ТИП 1: КВАДРАТ
1. Найдите сторону квадрата, диагональ которого
равна 14 .
.


-
14
2. Найдите площадь квадрата, если его диагональ равна 1.
-
0.5
3. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 16.
Найдите периметр этого квадрата.


-
128
ТИП 2:ПРЯМОУГОЛЬНИК
4. Найдите диагональ прямоугольника, две стороны которого
равны 24 и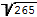 .
.

равны 24 и
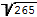 .
.
-
29
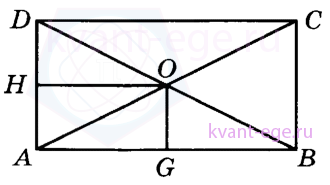
5. В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше,
чем расстояние от неё до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.

-
Давайте обозначим меньшую сторону прямоугольника как \( a \), а большую сторону как \( b \).
Согласно условию задачи, расстояние от точки пересечения диагоналей до меньшей стороны (которая соответствует \( a \)) на 1 больше, чем расстояние до большей стороны (которая соответствует \( b \)):
\[
\frac{a}{2} + 1 = \frac{b}{2}
\]
Это можно переписать как:
\[
b = a + 2
\]
Также из условия периметра известно, что:
\[
2a + 2b = 28
\]
Сокращая оба выражения на 2, получаем:
\[
a + b = 14
\]
Теперь подставим выражение для \( b \) из первого уравнения во второе. Получаем:
\[
a + (a + 2) = 14
\]
Упрощая, получаем:
\[
2a + 2 = 14
\]
\[
2a = 12
\]
\[
a = 6
\]
Таким образом, меньшая сторона прямоугольника равна \( 6 \).
Для проверки, подставим значение \( a \) в выражение для \( b \):
\[
b = a + 2 = 6 + 2 = 8
\]
Теперь проверим, выполняется ли условие про периметр:
\[
2a + 2b = 2(6) + 2(8) = 12 + 16 = 28
\]
Условия задачи выполняются, поэтому:
**Меньшая сторона прямоугольника равна 6.**
6. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и
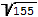 .
.

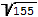 .
.
-
9
7. В прямоугольнике диагональ делит угол в отношении 1 : 2, меньшая его сторона равна 6.
Найдите диагональ данного прямоугольника.


-
12