ТИП 1: УГЛЫ ТРЕУГОЛЬНИК,УГЛЫ, БИССЕКТРИССЫ, ВНЕШНИЕ УГЛЫ
1.
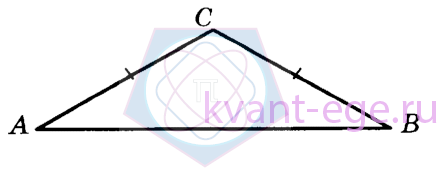
В треугольнике АВС угол А равен 29°, АС=ВС. Найдите угол С.
-
в равнобедренном треугольнике AC = BC, поэтому угол A равен углу B.
Обозначим угол B как \( x \). В таком случае, согласно свойству треугольника, сумма углов будет равна 180°:
\[
\angle A + \angle B + \angle C = 180°
\]
Так как угол A равен 29° и угол B также равен 29°, то:
\[
29° + 29° + \angle C = 180°
\]
Объединим углы:
\[
58° + \angle C = 180°
\]
Вычтем 58° из обеих сторон:
\[
\angle C = 180° - 58° = 122°
\]
Таким образом, угол C равен 122°.
2.
В треугольнике АВС угол С равен 20, АС=ВС. Найдите угол А. Отнет дайте в градусах.
-
Задача 2:
В треугольнике \(ABC\) угол \(C\) равен \(20^\circ\), а \(AC = BC\) (треугольник равнобедренный). Обозначим углы \(A\) и \(B\) как \(A\) и \(B\) соответственно. Используя свойство треугольника, можем записать:
\[
A + B + C = 180^\circ
\]
Так как треугольник равнобедренный, то \(A = B\). Подставим \(C\):
\[
2A + 20^\circ = 180^\circ
\]
Вычтем \(20^\circ\) из обеих сторон:
\[
2A = 160^\circ
\]
Теперь разделим на 2:
\[
A = 80^\circ
\]
Ответ: угол \(A\) равен \(80^\circ\).
3.
Углы треугольники относится как 1:6:11.Найдите больший из них. Ответ дайте в градусах.
-
Углы треугольника относятся как \(1:6:11\). Обозначим углы как \(x\), \(6x\), и \(11x\). Сумма углов треугольника равна \(180^\circ\):
\[
x + 6x + 11x = 180^\circ
\]
Сложим:
\[
18x = 180^\circ
\]
Разделим на 18:
\[
x = 10^\circ
\]
Теперь найдем большие углы:
- Первый угол: \(x = 10^\circ\)
- Второй угол: \(6x = 60^\circ\)
- Третий угол: \(11x = 110^\circ\)
Самый большой угол — это \(11x\):
Ответ: больший угол равен \(110^\circ\).
4.
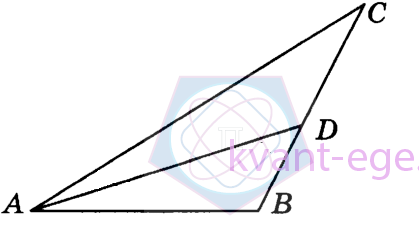
В треугольнике АВС угол С равен 30°, AD-биссектриса, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
-
52
5.
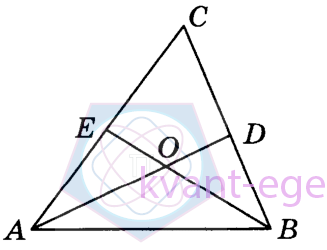
В треугольнике АВС угол С равен 148°, AD и BЕ биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
-
164
6.
В треугольнике АВС угол А равен 112°, внешний угол при вершине В равен 170°.Найдите угол С.Ответ дайте в градусах.
-
Угол A равен 112°, внешний угол при вершине B равен 170°. Внешний угол при вершине B равен сумме двух внутренних углов:
\[
\angle C + \angle A = 170° \Rightarrow \angle C = 170° - 112° = 58°.
\]
**Ответ:** 58°.
7.
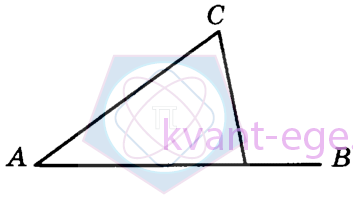
В треугольнике АВС угол А равен 53°, угол С равен 72°.Найдите внешний угол при вершине В.Ответ дайте в градусах.
-
Угол A равен 53°, угол C равен 72°. Чтобы найти внешний угол при вершине B, используем следующее:
Сумма углов в треугольнике:
\[
\angle A + \angle B + \angle C = 180°.
\]
Подставим известные значения:
\[
53° + B + 72° = 180° \Rightarrow B = 180° - 125° = 55°.
\]
Теперь, внешний угол при вершине B равен:
\[
180° - B = 180° - 55° = 125°.
\]
**Ответ:** 125°.
8.
В треугольнике АВС стороны АС и ВС равны, Внешний угол при вершине В равен 110°.Найдите угол С.Ответ дайте в градусах.
-
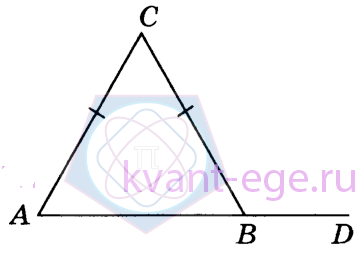
40
9.
В треугольнике АВС АВ=ВС, Внешний угол при вершине В ранен 170°.Найдите угол С.Ответ дайте в градусах.
-
AB=BC (равнобедренный треугольник), внешний угол при вершине B равен 170°. Пусть угол при вершине A равен A = C, тогда у нас:
\[
180° - B = 170° \Rightarrow B = 10°.
\]
Сумма углов:
\[
A + B + C = 180° \Rightarrow A + 10° + A = 180° \Rightarrow 2A = 170° \Rightarrow A = 85°.
\]
А, следовательно, угол C также равен:
\[
C = 85°.
\]
**Ответ:** 85°.
10.
Сумма двух углон треугольника и ннешнего угла к третьему рапна 144°.Найдите этот третий угол.Ответ дайте в градусах.
-
108
11.
В треугольнике АВС угол В равен 5°, угол С равен 47°, AD - биссектриса,E такая точка на АВ, что AE=AC.Найдите угол BDE.
Ответ дайте в градусах.
-
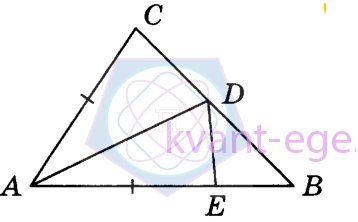
42
12.
В треугольнике АВС угол А равен 26°, угол В равен 76°, CD - биссектриса внешнего угла при вершине С,
причём точка D лежит на прямой АВ.На продолжении стороны АС за точку С выбрана такая точка Е, что CE=CB.
Найдите угол BDE. Ответ дайте в градусах.
-
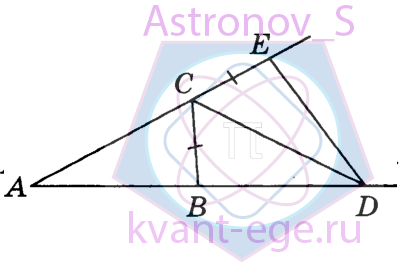
50
13.
В треугольнике АВС угол А равен 42°, угол С равен 20°. На продолжении стороны АВ за точку В отложен отрезок BD, ранный стороне ВС.
Найдите угол D треугольника BCD. Ответ дайте в градусах.
-
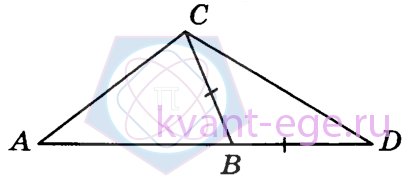
59
14.
В треугольнике АВС угол А равен 40°, внешний угол при вершине В равен 102°. Найдите угол С. Ответ дайте в градусах.
-
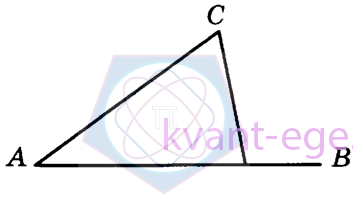
В треугольнике ABC угол A равен 40°, внешний угол при вершине B равен 102°. Мы знаем, что внешний угол равен сумме двух противолежащих внутренних углов:
\[
\text{внешний угол при B} = A + C \Rightarrow 102° = 40° + C \Rightarrow C = 102° - 40° = 62°
\]
Таким образом, угол C равен **62°**.
15. В треугольнике АВС АС=ВС, угол С равен 52°. Найдите внешний угол CBD. Ответ дайте в градусах.
-
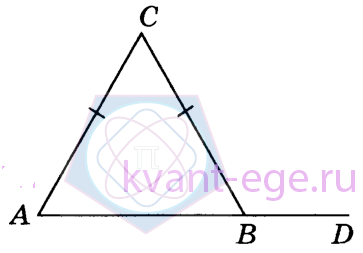
В треугольнике ABC, где AC = BC и угол C = 52°. Так как у нас равнобедренный треугольник, углы A и B равны:
\[
2x + C = 180° \Rightarrow 2x + 52° = 180°
\]
Решим уравнение:
\[
2x = 180° - 52° = 128° \Rightarrow x = 64°
\]
Таким образом, угол A равен B и равен **64°**. Внешний угол CBD будет равен:
\[
\angle CBD = 180° - B = 180° - 64° = 116°
\]
16.
Один из трёх углов равнобедренного треугольника равен 98°.Найдите один из других двух его углов. Ответ дайте в градусах.
-
В равнобедренном треугольнике один угол равен 98°. Пусть x - это другой равный угол:
\[
x + x + 98° = 180° \Rightarrow 2x = 180° - 98° = 82° \Rightarrow x = 41°
\]
Другие два угла равны **41°**.
17.
Один угол равнобедренного треугольника на 90° больше другого, Найдите меньший угол. Ответ дайте в градусах.
-
Один угол равнобедренного треугольника на 90° больше другого. Пусть меньший угол x, тогда больший угол будет x + 90°:
\[
x + (x + 90°) + x = 180° \Rightarrow 3x + 90° = 180° \Rightarrow 3x = 90° \Rightarrow x = 30°
\]
Меньший угол равен **30°**.
18.
В треугольнике АВC AD - биссектриса, угол С равен 50°, угол CAD равен 28°. Найдите угол В. Ответ дайте в градусах
-
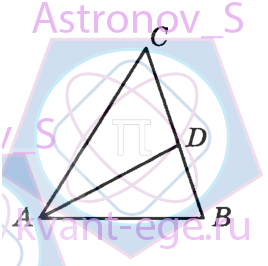
74
19.
В треугольнике АВС угол А равен 60°, угол В равен 33°. AD, BE и CF - биссектрисы, пересекающиеся в точке О.
Найдите угол АOF. Ответ дайте в градусах.
-
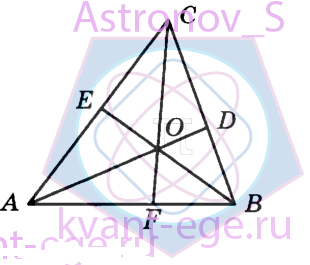
49
ТИП 2: ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. ВЫСОТЫ
20.
Один острый угол прямоугольного треугольника на 20° больше другого. Найдите больший острый угол. Ответ дайте в градусах.
-
Обозначим меньший угол как \(x\), тогда больший угол будет \(x + 20°\). Поскольку сумма острых углов в прямоугольном треугольнике равна 90°, мы можем записать уравнение:
\[
x + (x + 20°) = 90°
\]
Разрешая это уравнение:
\[
2x + 20° = 90° \\
2x = 70° \\
x = 35°
\]
Тогда больший угол:
\[
x + 20° = 35° + 20° = 55°
\]
**Ответ: 55°**
21.
Один острый угол прямоугольного треугольника в 3.5 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
-
Обозначим меньший угол как \(x\), тогда больший угол будет \(3.5x\). Сумма острых углов равна 90°:
\[
x + 3.5x = 90° \\
4.5x = 90° \\
x = 20°
\]
Тогда больший угол:
\[
3.5x = 3.5 \cdot 20° = 70°
\]
**Ответ: 70°**
22.
В треугольнике АВС угол С равен 90°, СН - высота, угол А равен 62°. Найдите угол ВСН. Ответ дайте в градусах.
-
62
23.
В треугольнике ABC AC=BC, AD-высота, угол BAD равен 55°. Найдите угол С. Ответ дайте в градусах.
-
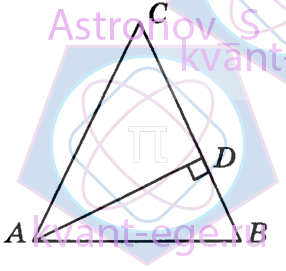
110
24.
В треугольнике АВС угол А равен 4°, СН - высота, угол ВСН равен 78°. Найдите угол АСВ. Ответ дайте в градусах.
-
8
25.
В треугольнике АВС угол А равен 7°, угол В равен 42°, СH - высота.
Найдите разность углов АСН и ВСН. Ответ дайте в градусах.
-
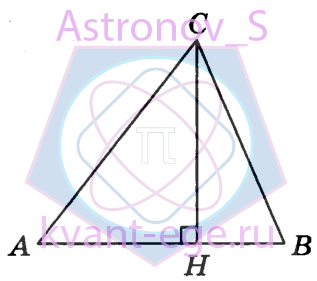
Угол A равен 7°, угол B равен 42°, найдите разность угол AСН и ВСН.
Углы AСН и ВСН можно найти как:
\[
\angle AСН = 90° - A = 90° - 7° = 83°\\
\angle ВСН = 90° - B = 90° - 42° = 48°
\]
Разность углов:
\[
\angle AСН - \angle ВСН = 83° - 48° = 35°
\]
**Ответ: 35°**
26.
В треугольнике АВС угол А равен 56°, углы В и С острые,
высоты BD и CЕ пересекаются в точке О. Найдите угол DOE. Ответ дайте в градусах.
-
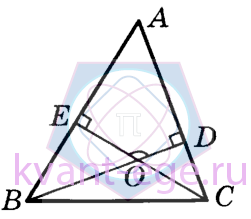
124
27.
В треугольнике АВС угол А равен 20°, угол В равен 35°. AD, BE и CF - высоты, пересекающиеся в точке O. Найдите угол AOF.
Ответ дайте в градусах.
-
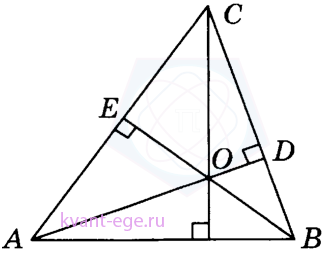
35
28.
В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 28°.
Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
-
59
29.
Острые углы прямоугольного треугольника равны 69° и 21°.
Найдите угол между биссектрисой и медианой, проведёнными из вершины прямого угла.
Ответ дайте в градусах.
-
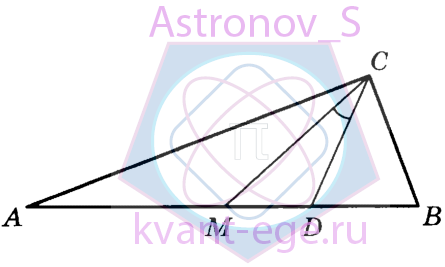
24
30.
В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 32°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
-
61
31.
В треугольнике АВС угол АСВ равен 90°, угол В равен 23°, CD - медиана. Найдите угол ACD. Ответ дайте в градусах.
-
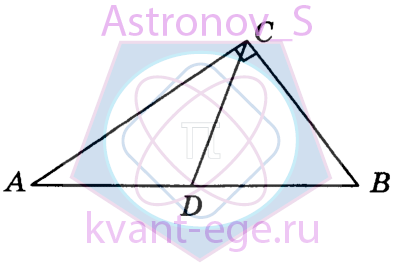
67
32.
В треугольнике АВС угол А равен 72°, BD и CE - высоты, пересекающиеся в точке О. Найдите угол DOE.
Ответ дайте в градусах.
-
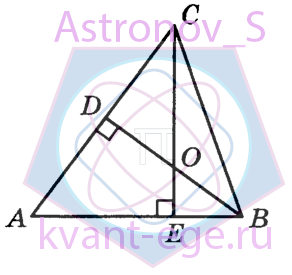
108
33.
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
-
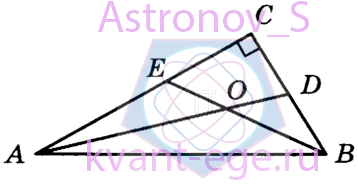
Используя базовые свойства треугольников:
\[
Угол = 90° - \left( \frac{A + B}{2} \right)\\
\angle = 45°\\
\]
**Ответ: 45°**
34.
Острые углы прямоугольного треугольника равны 29° и 61°. Найдите угол между высотой и биссектрисой,
проведёнными из вершины прямого угла. Ответ дайте в градусах.
-
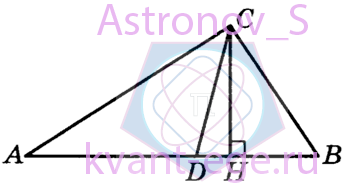
16
35. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой,
проведёнными из вершины прямого угла. Ответ дайте в градусах.
-
21
ТИП 3: ПЛОЩАДЬ. ПОДОБИЕ
36.
Катеты прямоугольного треугольника равны 12 и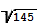 
.Найдите гипотенузу.
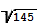.Найдите гипотенузу.
-
17
37.
Гипотенуза прямоугольного треугольника равна 38. Один из его катетов равен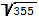
.
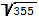Найдите другой катет.
.
Найдите другой катет.-
33
38.
Найдите площадь прямоугольного треугольника, если его катеты равны 11 и 2.
-
Площадь треугольника вычисляется по формуле:
\[
S = \frac{1}{2} \cdot a \cdot b
\]
где \(a = 11\) и \(b = 2\):
\[
S = \frac{1}{2} \cdot 11 \cdot 2 = 11.
\]
**Ответ: 11.**
39.
В треугольнике со сторонами 18 и 6 проведены высоты к этим сторонам. Высота, проведённая к первой из
этих сторон, равна 1. Чему равна высота, проведённая ко второй стороне?
-
Площадь \(S\) треугольника можно выразить через высоты:
\[
S = \frac{1}{2} \cdot a \cdot h_a = \frac{1}{2} \cdot b \cdot h_b,
\]
где \(a = 18\), \(b = 6\), \(h_a = 1\).
Сначала найдем площадь:
\[
S = \frac{1}{2} \cdot 18 \cdot 1 = 9.
\]
Теперь находим высоту \(h_b\):
\[
9 = \frac{1}{2} \cdot 6 \cdot h_b \Rightarrow h_b = \frac{9 \cdot 2}{6} = 3.
\]
**Ответ: 3.**
40.
Найдите площадь треугольника, две стороны которого равны 34 и 8, а угол между ними равен 30°.
-
Для нахождения площади треугольника, когда известны две стороны \( a \) и \( b \) и угол \( \theta \) между ними, можно воспользоваться формулой:
\[
S = \frac{1}{2} \times a \times b \times \sin(\theta)
\]
В нашем случае:
- \( a = 34 \)
- \( b = 8 \)
- \( \theta = 30^\circ \)
Сначала найдем значение синуса угла 30°:
\[
\sin(30^\circ) = \frac{1}{2}
\]
Теперь подставим все известные величины в формулу:
\[
S = \frac{1}{2} \times 34 \times 8 \times \frac{1}{2}
\]
Упростим это выражение:
\[
S = \frac{1}{2} \times 34 \times 8 \times 0.5 = \frac{34 \times 8}{4} = \frac{272}{4} = 68
\]
Таким образом, площадь треугольника равна \( 68 \) квадратных единиц.
41.
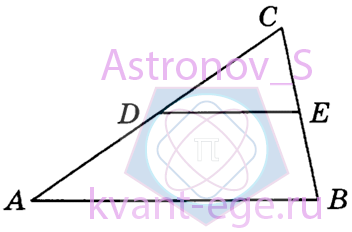
Площадь треугольника АBС равна 200. DE - средняя линия.
Найдите площадь треугольника CDE.
-
Площадь треугольника, образованного средней линией, равна половине площади треугольника \(ABC\):
\[
S_{CDE} = \frac{1}{4} \cdot S_{ABC} = \frac{1}{4} \cdot 200 = 50.
\]
**Ответ: 50.**
42.
В треугольнике ABC DE - средняя линия.
Площадь треугольника ADE равна 4. Найдите площадь треугольника АВС.
-
16
43.
Площадь треугольника АBС равна 40.
DE - средняя линия,параллельная стороне АВ.
Найдите площадь трапеции АВED
-
. Площадь треугольника ABC равна 40. DE - средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Площадь трапеции равна площади треугольника \(ABC\) минус площадь треугольника \(CDE\), который равен половине площади \(ABC\):
\[
S_{CDE} = \frac{1}{4} \cdot S_{ABC} = \frac{1}{4} \cdot 40 = 10.
\]
Значит, площадь трапеции:
\[
S_{ABED} = S_{ABC} - S_{CDE} = 40 - 10 = 30.
\]
**Ответ: 30.**