ПИРАМИДА
5.4.1
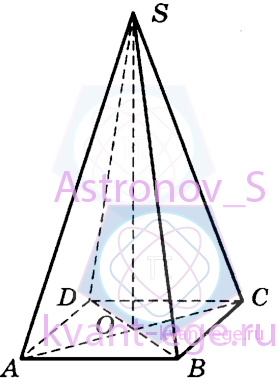
В правильной четырёхугольной пирамиде SABCD точка О-центр основания,
S - вершина, SA = 13, BD = 10.
Найдите длину отрезка SO.

-
12
5.4.2
B правильной четырёхугольной пирамиде SABCD точка O -
центр основания, S вершина, SO = 7 AC = 48. Найдите боковое ребро SB.
-
25
5.4.3
B правильной четырёхугольной пирамиде SABCD точка O - центр основания,
S вершина, SO = 24, SC = 25. Найдите длину отрезка BD.
-
14
5.4.4
В правильной четырёхугольной пирамиде высота равна 2,
боковое ребро равно 8. Найдите её объём.
-
80
5.4.5
Найдите площадь поверхности правильной четырёхугольной пирамиды,
стороны основания которой равны 6 и высота равна 4.

-
96
5.4.6
Стороны основания правильной четырёхугольной пирамиды равны 6, боковые рёбра равны 5. Найдите площадь поверхности этой пирамиды.
-
84
5.4.7
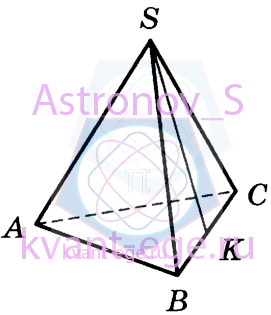
В правильной треугольной пирамиде SABC точка К - середина ребра ВС, S - вершина. Известно, что
AB = 6, а длина отрезка SK = 7. Найдите площадь боковой поверхности пирамиды.

-
63
5.4.8
В правильной треугольной пирамиде SABC точка М - середина ребра ВС, S - вершина.
Известно, что АB = 6, а площадь боковой поверхности равна 45. Найдите длину отрезка SM.
-
8
5.4.9
Найдите объём правильной треугольной пирамиды, стороны основания которой равны 1, а высота
равна .
.

-
0,25
5.4.10
В правильной треугольной пирамиде SABC медианы
основания пересекаются в точке P. Площадь треугольника АВС равна 8, объём пирамиды равен 48.
Найдите длину отрезка PS.
-
18
5.4.11
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке К. Объём пирамиды равен 80, KS = 15. Найдите площадь треугольника
АВС.
-
16
5.4.12
Во сколько раз увеличится площадь поверхности октаэдра, если все его рёбра увеличить в 26 раз?


-
676
5.4.13
В правильной четырёхугольной пирамиде все рёбра равны 5.
Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

-
6,25
5.4.14
Во сколько раз увеличится площадь поверхности пирамиды, если все её ребра увеличить в 2 раза?


-
4
5.4.15
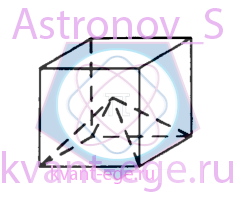
Объём куба равен 123.
Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной - центр куба.

-
450
СЛОЖНЫЕ
5.4.16
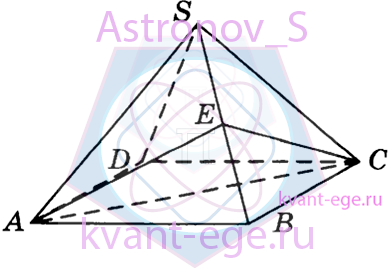
Объём правильной четырехугольной пирамиды SABCD равен 132.
Точка Е - середина ребра SB. Найдите объём треугольной пирамиды ЕАВС.

-
33
5.4.17
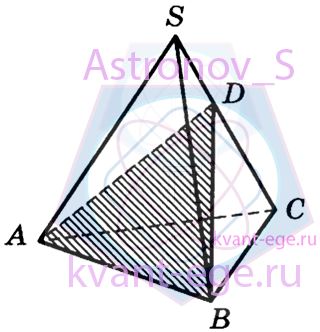
Объём треугольной пирамиды SABC равен 15.
Плоскость проходит через сторону АВ основания этой пирамиды и пересекает противоположное
боковое ребро в точке D, делящей ребро SC в отношении 1 : 2, считая от вершины S. Найдите объём пирамиды DABC.

-
10
5.4.18
От треугольной пирамиды, объём которой равен 38,отсечена треугольная пирамида плоскостью,
проходящей через вершину пирамиды и среднюю линию основания. Найдите объём отсечённой треугольной пира-
миды.


-
9,5
5.4.19
Объём тетраэдра равен 1,2. Найдите объём многогранника, вершинами которого являются середины сторон данного тетраэдра.


-
0,6
5.4.20
Площадь поверхности тетраэдра равна 1,3. Найдите площадь поверхности многогранника,
вершинами которого являются середины сторон данного тетраэдра.


-
0,65
5.4.21
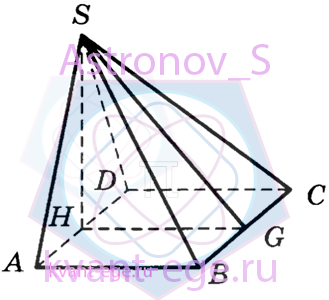
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания,
а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объём пирамиды.

-
48
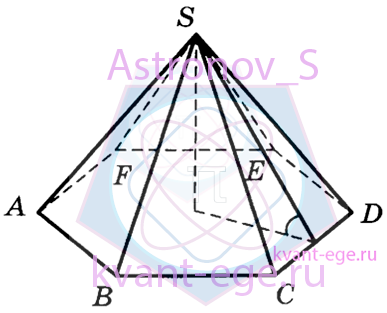
5.4.22
Сторона основания правильной шестиугольной пирамиды равна 4,
а угол между боковой гранью и основанием равен 45°. Найдите объём пирамиды.

-
48
5.4.23
Объём треугольной пирамиды равен 30.
Плоскость проходит через сторону основания этой пирамиды
и пересекает противоположное боковое ребро в точке, делящей его в отношении 7:3,
считая от вершины пирамиды.
Найдите больший из объёмов пирамид,на которые плоскость разбивает исходную пирамиду.
-
21