Конус
1
Высота конуса равна 7, а диаметр основания - 48.
Найдите образующую конуса.


-
Дано: высота \( h = 7 \), диаметр основания \( d = 48 \). Радиус основания \( r = \frac{d}{2} = \frac{48}{2} = 24 \).
Образующая \( l \) конуса может быть найдена по формуле:
\[
l = \sqrt{h^2 + r^2}
\]
Подставляем значения:
\[
l = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25
\]
Таким образом, образующая конуса равна **25**.
2
Высота конуса равна 5, а длина образующей - 13.
Найдите диаметр основания конуса.
-
Дано: высота \( h = 5 \), длина образующей \( l = 13 \).
Используем ту же формулу для образующей:
\[
l = \sqrt{h^2 + r^2}
\]
Из нее найдем радиус \( r \):
\[
13 = \sqrt{5^2 + r^2}
\]
Возведем в квадрат:
\[
169 = 25 + r^2 \implies r^2 = 169 - 25 = 144 \implies r = 12
\]
Диаметр \( d = 2r = 2 \times 12 = 24 \).
Таким образом, диаметр основания конуса равен **24**.
3
Диаметр основания конуса равен 14, a длина образующей - 25.
Найдите высоту конуса.
-
Дано: диаметр основания \( d = 14 \), длина образующей \( l = 25 \). Радиус основания \( r = \frac{d}{2} = 7 \).
Используем формулу для образующей:
\[
l = \sqrt{h^2 + r^2}
\]
Находим высоту:
\[
25 = \sqrt{h^2 + 7^2}
\]
Возводим в квадрат:
\[
625 = h^2 + 49 \implies h^2 = 625 - 49 = 576 \implies h = 24
\]
Таким образом, высота конуса равна **24**.
Объем конуса
.
4
Высота конуса равна 6, образующая равна 10.
Найдите его объём, делённый на π.


-
Дано: высота \( h = 6 \), образующая \( l = 10 \) (радиус не нужен, так как не используется в формуле). Поскольку радиус не задан, мы используем формулу объема:
\[
V = \frac{1}{3} \pi r^2 h
\]
Сначала найдем радиус, используя образующую:
\[
l = \sqrt{h^2 + r^2} \implies 10 = \sqrt{6^2 + r^2}
\]
Возводим в квадрат:
\[
100 = 36 + r^2 \implies r^2 = 64 \implies r = 8
\]
Теперь вычислим объем:
\[
V = \frac{1}{3} \pi (8^2) (6) = \frac{1}{3} \pi (64)(6) = \frac{1}{3} \pi (384) = 128\pi
\]
Делим результат на \( \pi \):
\[
\frac{V}{\pi} = 128
\]
Таким образом, объем конуса, деленный на \( \pi \), равен **128**.
5
Во сколько раз увеличится объём конуса,
если радиус его основания увеличить в 1,5 раза?
-
**Во сколько раз увеличится объем конуса, если радиус его основания увеличить в 1,5 раза?**
Объем конуса определяется формулой \( V = \frac{1}{3} \pi r^2 h \). Если радиус увеличивается в 1,5 раза, то объем увеличивается в \( (1.5^2) = 2.25 \) раза.
Таким образом, объем увеличится в **2.25** раза.
6
Во сколько раз уменьшится объём конуса,
если его высота уменьшится в 18,5 раза, а радиус основания останется прежним?
-
Объем конуса определяется формулой \( V = \frac{1}{3} \pi r^2 h \).
Если высота уменьшается в 18,5 раз, объем уменьшится в 18,5 раз.
Таким образом, объем уменьшится в **18.5** раз.
7
Во сколько раз увеличится объём конуса, если радиус его
основания увеличится в 1,5 раза, а высота останется прежней?
-
Объем конуса определяется по формуле:
\[
V = \frac{1}{3} \pi r^2 h
\]
Где:
- \( r \) — радиус основания конуса,
- \( h \) — высота конуса.
Если радиус основания увеличивается в 1,5 раза, то новый радиус станет \( r' = 1.5r \). Высота остается прежней, то есть \( h' = h \).
Тогда новый объем конуса будет:
\[
V' = \frac{1}{3} \pi (1.5r)^2 h = \frac{1}{3} \pi (2.25r^2) h = 2.25 \cdot \frac{1}{3} \pi r^2 h = 2.25 V
\]
Таким образом, объем конуса увеличится в \( 2.25 \) раза.
8
Диаметр основания конуса равен 14, а длина образующей - 25.
Найдите площадь осевого сечения этого конуса.


-
Площадь осевого сечения конуса — это треугольник, основание которого равно диаметру основания конуса, а высота равна высоте конуса.
Сначала найдем высоту конуса по теореме Пифагора:
- Половина диаметра основания: \( r = \frac{14}{2} = 7 \)
- Длина образующей (гипотенуза) \( l = 25 \)
В соответствии с теоремой Пифагора:
\[
h = \sqrt{l^2 - r^2} = \sqrt{25^2 - 7^2} = \sqrt{625 - 49} = \sqrt{576} = 24
\]
Теперь находим площадь осевого сечения:
\[
S = \frac{1}{2} \cdot основание \cdot высота = \frac{1}{2} \cdot 14 \cdot 24 = 168
\]
9
Высота конуса равна 12, а длина образующей - 37.
Найдите площадь осевого сечения этого конуса.
-
Здесь высота конуса \( h = 12 \) и длина образующей \( l = 37 \).
Находим радиус основания с помощью теоремы Пифагора:
\[
r = \sqrt{l^2 - h^2} = \sqrt{37^2 - 12^2} = \sqrt{1369 - 144} = \sqrt{1225} = 35
\]
Теперь находим площадь осевого сечения:
\[
S = \frac{1}{2} \cdot основание \cdot высота = \frac{1}{2} \cdot (2r) \cdot h = \frac{1}{2} \cdot (2 \cdot 35) \cdot 12 = 35 \cdot 12 = 420
\]
Площадь боковой поверхности
10
Радиус основания конуса равен 3, высота равна 4.
Найдите площадь поверхности конуса, делённую на π.


-
Для нахождения площади поверхности конуса мы используем следующую формулу:
\[
S = S_{\text{основания}} + S_{\text{боковая}}
\]
где:
1. Площадь основания \( S_{\text{основания}} = \pi r^2 \)
2. Площадь боковой поверхности \( S_{\text{боковая}} = \pi r l \)
3. \( l \) — образующая конуса, которая рассчитывается по теореме Пифагора: \( l = \sqrt{r^2 + h^2} \)
Теперь подставим известные значения:
- Радиус основания \( r = 3 \)
- Высота \( h = 4 \)
1. Вычислим образующую:
\[
l = \sqrt{r^2 + h^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
2. Площадь основания:
\[
S_{\text{основания}} = \pi r^2 = \pi \cdot 3^2 = \pi \cdot 9
\]
3. Площадь боковой поверхности:
\[
S_{\text{боковая}} = \pi r l = \pi \cdot 3 \cdot 5 = 15\pi
\]
4. Полная площадь поверхности:
\[
S = S_{\text{основания}} + S_{\text{боковая}} = 9\pi + 15\pi = 24\pi
\]
Теперь, делим площадь поверхности на \( \pi \):
\[
\frac{S}{\pi} = 24
\]
Таким образом, площадь поверхности конуса, делённая на \( \pi \), равна:
\[
\boxed{24}
\]
11
Во сколько раз увеличится площадь боковой поверхности конуса,
если его образующую увеличить в 3 раза?
-
Площадь боковой поверхности конуса рассчитывается по формуле:
\[
S_{б} = \pi r l
\]
Если образующая увеличивается в 3 раза, то \( l' = 3l \). Радиус остается прежним.
Новая площадь боковой поверхности:
\[
S_{б}' = \pi r \cdot (3l) = 3 \cdot (\pi r l) = 3S_{б}
\]
Следовательно, площадь боковой поверхности увеличится в 3 раза.
12
Высота конуса равна 6, образующая равна 10.
Найдите площадь его поверхности, делённую на π.
-
Площадь поверхности конуса включает площадь основания и боковую поверхность.
1. Радиус основания (r) найдем по теореме Пифагора:
\[
l^2 = h^2 + r^2 \Rightarrow 10^2 = 6^2 + r^2 \Rightarrow 100 = 36 + r^2 \Rightarrow r^2 = 64 \Rightarrow r = 8
\]
2. Площадь основания:
\[
S_{\text{основания}} = \pi r^2 = \pi \cdot 8^2 = 64\pi
\]
3. Площадь боковой поверхности:
\[
S_{\text{боковая}} = \pi r l = \pi \cdot 8 \cdot 10 = 80\pi
\]
4. Полная площадь поверхности:
\[
S = S_{\text{основания}} + S_{\text{боковая}} = 64\pi + 80\pi = 144\pi
\]
Таким образом, площадь поверхности конуса, делённая на π, равна:
\[
\boxed{144}
\]
13
Во сколько раз увеличится площадь боковой поверхности конуса,
если его образующая увеличится в 11 раз,
а радиус основания останется прежним?


-
Во сколько раз увеличится площадь боковой поверхности конуса при увеличении образующей в 11 раз.
Площадь боковой поверхности конуса:
\[
S_{\text{боковая}} = \pi r l
\]
Если образующая увеличится в 11 раз:
\[
l' = 11l
\]
Площадь боковой поверхности станет:
\[
S'_{\text{боковая}} = \pi r l' = \pi r (11l) = 11 (\pi r l) = 11 S_{\text{боковая}}
\]
Следовательно, площадь боковой поверхности увеличится в 11 раз:
\[
\boxed{11}
\]
14
Во сколько раз уменьшится площадь боковой поверхности конуса,
если радиус его основания уменьшится в 8 раз,
а образующая останется прежней?
-
Во сколько раз уменьшится площадь боковой поверхности, если радиус уменьшится в 8 раз, а образующая останется прежней.
Если радиус уменьшается в 8 раз:
\[
r' = \frac{r}{8}
\]
Площадь боковой поверхности изменится так:
\[
S'_{\text{боковая}} = \pi r' l = \pi \left(\frac{r}{8}\right) l = \frac{1}{8} (\pi r l) = \frac{1}{8} S_{\text{боковая}}
\]
Площадь боковой поверхности уменьшится в 8 раз:
\[
\boxed{8}
\]
15
Длина окружности основания конуса равна 7,
образующая равна 2. Найдите площадь боковой поверхности конуса.
-
Длина окружности:
\[
C = 2\pi r \Rightarrow r = \frac{C}{2\pi} = \frac{7}{2\pi}
\]
Площадь боковой поверхности:
\[
S_{\text{боковая}} = \pi r l = \pi \left(\frac{7}{2\pi}\right) \cdot 2 = 7
\]
Таким образом, площадь боковой поверхности равна:
\[
\boxed{7}
\]
Подобие
16
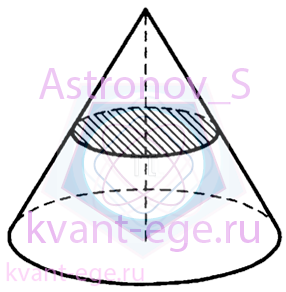
Объём конуса равен 48.
Через середину высоты параллельно основанию конуса проведено сечение,
которое является основанием меньшего конуса с той же вершиной.
Найдите объём меньшего конуса.

-
Объём конуса можно выразить формулой:
\[
V = \frac{1}{3} S_{осн} h
\]
где \( S_{осн} \) — площадь основания, \( h \) — высота конуса.
Пусть высота исходного конуса равна \( h \) и радиус основания равен \( r \). Тогда объём конуса равен:
\[
V = \frac{1}{3} \pi r^2 h
\]
Из условия задачи известно, что \( V = 48 \):
\[
\frac{1}{3} \pi r^2 h = 48
\]
Теперь рассматриваем сечение, проведённое через середину высоты конуса. Высота меньшего конуса составит \( \frac{h}{2} \).
Поскольку сечение проведено параллельно основанию, радиус основания меньшего конуса также уменьшится вдвое, и составит \( \frac{r}{2} \).
Теперь найдём объём меньшего конуса:
\[
V_{меньший} = \frac{1}{3} \pi \left(\frac{r}{2}\right)^2 \left(\frac{h}{2}\right)
\]
В этом выражении можно упростить:
\[
V_{меньший} = \frac{1}{3} \pi \frac{r^2}{4} \cdot \frac{h}{2} = \frac{1}{3} \pi r^2 h \cdot \frac{1}{8} = \frac{1}{8} \left(\frac{1}{3} \pi r^2 h\right)
\]
Мы знаем, что \( \frac{1}{3} \pi r^2 h = 48 \):
\[
V_{меньший} = \frac{1}{8} \cdot 48 = 6
\]
Таким образом, объём меньшего конуса равен \( \boxed{6} \).
17
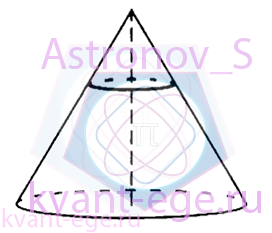
Площадь основания конуса равна 144.
Плоскость, параллельная плоскости основания конуса,
делит его высоту на отрезки длиной 11 и 33,
считая от вершины.
Найдите площадь сечения конуса этой плоскостью.

-
9
18
В сосуд, имеющий форму конуса, налили 25 мл жидкости до
половины высоты сосуда.
Сколько миллилитров жидкости нужно долить в сосуд,
чтобы заполнить его доверху?


-
175
19
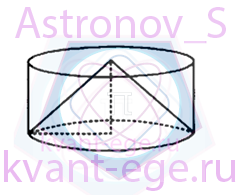
Цилиндр и конус имеют общее основание и общую высоту.
Найдите объём цилиндра, если объём конуса равен 20.

-
Объём конуса:
\[
V_{\text{конус}} = \frac{1}{3} \pi r^2 h = 20
\]
Объём цилиндра:
\[
V_{\text{цилиндр}} = \pi r^2 h
\]
Объём цилиндра в 3 раза больше, чем объём конуса:
\[
V_{\text{цилиндр}} = 3 \cdot 20 = 60
\]
Таким образом, объём цилиндра равен:
\[
\boxed{60}
\]
20
Цилиндр и конус имеют общие основание и высоту.
Высота цилиндра равна радиусу основания.
Площадь боковой поверхности цилиндра равна
11 .
Найдите площадь боковой поверхности конуса.
.
Найдите площадь боковой поверхности конуса.
-
Площадь боковой поверхности цилиндра:
\[
S_{\text{цилиндра}} = 11\sqrt{2}
\]
Площадь боковой поверхности цилиндра:
\[
S_{\text{цилиндра}} = 2\pi rh
\]
Поскольку высота равна радиусу:
\[
S_{\text{ц}} = 2\pi r^2
\]
\[
2\pi r^2 = 11\sqrt{2} \Rightarrow r^2 = \frac{11\sqrt{2}}{2\pi}
\]
Площадь боковой поверхности конуса:
\[
S_{\text{конуса}} = \pi r l
\]
где \( l = \sqrt{r^2 + h^2} = \sqrt{r^2 + r^2} = \sqrt{2r^2} = r\sqrt{2} \)
Тогда:
\[
S_{\text{конуса}} = \pi r^2\sqrt{2} = \sqrt{2} \cdot \frac{11\sqrt{2}}{2\pi} = \frac{11 \cdot 2}{2} = 11
\]
Таким образом, площадь боковой поверхности конуса равна:
\[
\boxed{11}
\]