Степенные уравнения ЕГЭ ОГЭ
ТИП 1
1.
Найдите корень уравнения:
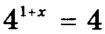
Ответ:
Чтобы решить уравнение \( 4^{(x+1)} = 4 \), сначала заметим, что \( 4 \) можно записать как \( 4^1 \). Таким образом, уравнение можно переписать как:
\[
4^{(x+1)} = 4^1
\]
Теперь, поскольку основания равны, можно приравнять показатели степени:
\[
x + 1 = 1
\]
Теперь решаем это уравнение:
\[
x = 1 - 1
\]
\[
x = 0
\]
Ответ: \( x = 0 \).
2.
Найдите корень уравнения:
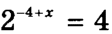
Ответ:
6
3.
Найдите корень уравнения:
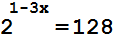
Ответ:
-2
4.
Найдите корень уравнения:
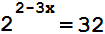
Ответ:
-1
ТИП 2
5.
Найдите корень уравнения:
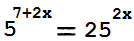
Ответ:
Чтобы решить уравнение \( 5^{(2x+7)} = 25^{(2x)} \), сначала преобразуем \( 25 \) в степень с основанием \( 5 \):
\[
25 = 5^2
\]
Таким образом, можем записать наше уравнение следующим образом:
\[
5^{(2x+7)} = (5^2)^{(2x)}
\]
Согласно правилам степеней, мы можем упростить правую сторону:
\[
(5^2)^{(2x)} = 5^{(2 \cdot 2x)} = 5^{(4x)}
\]
Теперь у нас получается следующее уравнение:
\[
5^{(2x+7)} = 5^{(4x)}
\]
Так как основания равны, мы можем приравнять показатели степени:
\[
2x + 7 = 4x
\]
Теперь решим это уравнение:
1. Переносим \( 2x \) на правую сторону:
\[
7 = 4x - 2x
\]
2. Упрощаем:
\[
7 = 2x
\]
3. Делим обе стороны на 2:
\[
x = \frac{7}{2}
\]
Таким образом, решение уравнения:
\[
x = 3.5
\]
6.
Найдите корень уравнения:
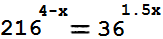
Ответ:
2
ТИП 3
7.
Найдите корень уравнения:
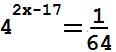
Ответ:
Чтобы решить уравнение \( 4^{(2x-17)} = \frac{1}{64} \), сначала преобразим правую сторону уравнения.
Мы знаем, что \( 64 = 4^3 \), следовательно, \( \frac{1}{64} = 4^{-3} \). Таким образом, уравнение можно переписать как:
\[
4^{(2x-17)} = 4^{-3}
\]
Так как основания (4) равны, можно приравнять показатели степеней:
\[
2x - 17 = -3
\]
Теперь решим это уравнение:
1. Сначала добавим 17 к обеим сторонам:
\[
2x = -3 + 17
\]
2. Упрощаем:
\[
2x = 14
\]
3. Теперь делим обе стороны на 2:
\[
x = 7
\]
Таким образом, решение уравнения:
\[
x = 7
\]
8.
Найдите корень уравнения:
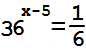
Ответ:
4,5
9.
Найдите корень уравнения:
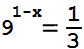
Ответ:
1,5
ТИП 4
10.
Найдите корень уравнения:
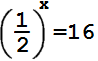
Ответ:
Чтобы решить уравнение \(\frac{1}{2^{x}} = 16\), сначала преобразим правую сторону уравнения, выразив \(16\) как степень двойки:
\[
16 = 2^4.
\]
Теперь, перепишем уравнение:
\[
\frac{1}{2^{x}} = 2^4.
\]
Вспомнив, что \(\frac{1}{a} = a^{-1}\), мы можем переписать левую часть:
\[
2^{-x} = 2^4.
\]
Поскольку основания равны, мы можем приравнять показатели степени:
\[
-x = 4.
\]
Теперь, чтобы найти \(x\), умножим обе стороны на \(-1\):
\[
x = -4.
\]
Таким образом, решение уравнения:
\[
x = -4.
\]
11.
Найдите корень уравнения:
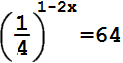
Ответ:
2
12.
Найдите корень уравнения:
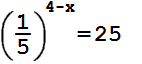
Ответ:
8
ТИП 5
13.
Найдите корень уравнения:
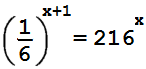
Ответ:
To solve the equation
\[
\frac{1}{6^{(x+1)}} = 216^{(x)},
\]
we can start by rewriting both sides using the same base. First, let's express 216 in terms of its prime factors:
\[
216 = 6^3,
\]
so we can rewrite \(216^x\) as
\[
216^x = (6^3)^x = 6^{3x}.
\]
Now, substituting this back into the equation gives us:
\[
\frac{1}{6^{(x+1)}} = 6^{3x}.
\]
Next, we can rewrite \(\frac{1}{6^{(x+1)}}\) as \(6^{-(x+1)}\), leading to:
\[
6^{-(x+1)} = 6^{3x}.
\]
Since the bases are the same, we can set the exponents equal to each other:
\[
-(x+1) = 3x.
\]
Now, we can solve for \(x\):
\[
-x - 1 = 3x.
\]
Adding \(x\) to both sides gives:
\[
-1 = 4x.
\]
Dividing both sides by 4 results in:
\[
x = -\frac{1}{4}.
\]
Thus, the solution to the equation \(\frac{1}{6^{(x+1)}} = 216^{(x)}\) is
\[
\boxed{-\frac{1}{4}}.
\]
14.
Найдите корень уравнения:
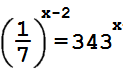
Ответ:
0,5
15.
Найдите корень уравнения:
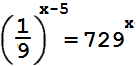
Ответ:
1,25
Тип 6
16.
Найдите корень уравнения:
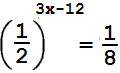
Ответ:
5
17.
Найдите корень уравнения:
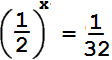
Ответ:
Давайте решим уравнение:
\[
\frac{1}{2^{(x)}} = \frac{1}{32}.
\]
Для начала, заметим, что \(32\) можно выразить через степень \(2\):
\[
32 = 2^5.
\]
Таким образом, мы можем переписать правую часть уравнения:
\[
\frac{1}{32} = \frac{1}{2^5}.
\]
Теперь уравнение выглядит так:
\[
\frac{1}{2^x} = \frac{1}{2^5}.
\]
Поскольку обе части имеют одну и ту же основу, мы можем приравнять показатели:
\[
-x = -5.
\]
Умножив обе стороны на \(-1\), получаем:
\[
x = 5.
\]
Таким образом, решение уравнения:
\[
\boxed{5}.
\]
Тип 7
18.
Найдите корень уравнения:
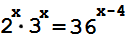
Ответ:
Для решения уравнения
\[
2^{(x)} \cdot 3^{(x)} = 36^{(x-4)},
\]
начнем с того, что \(36\) можно выразить через множители \(2\) и \(3\):
\[
36 = 6^2 = (2 \cdot 3)^2 = 2^2 \cdot 3^2.
\]
Таким образом, мы можем записать \(36^{(x-4)}\) как:
\[
36^{(x-4)} = (2^2 \cdot 3^2)^{(x-4)} = 2^{2(x-4)} \cdot 3^{2(x-4)} = 2^{(2x-8)} \cdot 3^{(2x-8)}.
\]
Теперь подставим это в исходное уравнение:
\[
2^{(x)} \cdot 3^{(x)} = 2^{(2x-8)} \cdot 3^{(2x-8)}.
\]
Теперь, так как основание одинаковое, мы можем приравнять показатели:
1. Для оснований \(2\):
\[
x = 2x - 8.
\]
Решим это уравнение:
\[
x - 2x = -8 \implies -x = -8 \implies x = 8.
\]
2. Для оснований \(3\):
\[
x = 2x - 8.
\]
Аналогично, мы получаем:
\[
x - 2x = -8 \implies -x = -8 \implies x = 8.
\]
Таким образом, для обоих случаев мы получаем одно и то же значение для \(x\).
В итоге, решение уравнения:
\[
\boxed{8}.
\]
19.
Найдите корень уравнения:
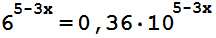
Ответ:
1
20.
Найдите корень уравнения:
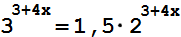
Ответ:
-0,5
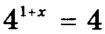
-
Чтобы решить уравнение \( 4^{(x+1)} = 4 \), сначала заметим, что \( 4 \) можно записать как \( 4^1 \). Таким образом, уравнение можно переписать как:
\[
4^{(x+1)} = 4^1
\]
Теперь, поскольку основания равны, можно приравнять показатели степени:
\[
x + 1 = 1
\]
Теперь решаем это уравнение:
\[
x = 1 - 1
\]
\[
x = 0
\]
Ответ: \( x = 0 \).
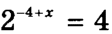
-
6
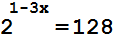
-
-2
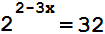
-
-1
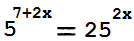
-
Чтобы решить уравнение \( 5^{(2x+7)} = 25^{(2x)} \), сначала преобразуем \( 25 \) в степень с основанием \( 5 \):
\[
25 = 5^2
\]
Таким образом, можем записать наше уравнение следующим образом:
\[
5^{(2x+7)} = (5^2)^{(2x)}
\]
Согласно правилам степеней, мы можем упростить правую сторону:
\[
(5^2)^{(2x)} = 5^{(2 \cdot 2x)} = 5^{(4x)}
\]
Теперь у нас получается следующее уравнение:
\[
5^{(2x+7)} = 5^{(4x)}
\]
Так как основания равны, мы можем приравнять показатели степени:
\[
2x + 7 = 4x
\]
Теперь решим это уравнение:
1. Переносим \( 2x \) на правую сторону:
\[
7 = 4x - 2x
\]
2. Упрощаем:
\[
7 = 2x
\]
3. Делим обе стороны на 2:
\[
x = \frac{7}{2}
\]
Таким образом, решение уравнения:
\[
x = 3.5
\]
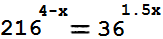
-
2
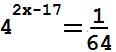
-
Чтобы решить уравнение \( 4^{(2x-17)} = \frac{1}{64} \), сначала преобразим правую сторону уравнения.
Мы знаем, что \( 64 = 4^3 \), следовательно, \( \frac{1}{64} = 4^{-3} \). Таким образом, уравнение можно переписать как:
\[
4^{(2x-17)} = 4^{-3}
\]
Так как основания (4) равны, можно приравнять показатели степеней:
\[
2x - 17 = -3
\]
Теперь решим это уравнение:
1. Сначала добавим 17 к обеим сторонам:
\[
2x = -3 + 17
\]
2. Упрощаем:
\[
2x = 14
\]
3. Теперь делим обе стороны на 2:
\[
x = 7
\]
Таким образом, решение уравнения:
\[
x = 7
\]
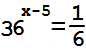
-
4,5
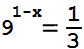
-
1,5
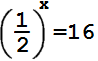
-
Чтобы решить уравнение \(\frac{1}{2^{x}} = 16\), сначала преобразим правую сторону уравнения, выразив \(16\) как степень двойки:
\[
16 = 2^4.
\]
Теперь, перепишем уравнение:
\[
\frac{1}{2^{x}} = 2^4.
\]
Вспомнив, что \(\frac{1}{a} = a^{-1}\), мы можем переписать левую часть:
\[
2^{-x} = 2^4.
\]
Поскольку основания равны, мы можем приравнять показатели степени:
\[
-x = 4.
\]
Теперь, чтобы найти \(x\), умножим обе стороны на \(-1\):
\[
x = -4.
\]
Таким образом, решение уравнения:
\[
x = -4.
\]
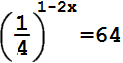
-
2
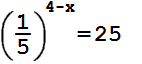
-
8
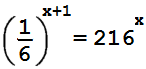
-
To solve the equation
\[
\frac{1}{6^{(x+1)}} = 216^{(x)},
\]
we can start by rewriting both sides using the same base. First, let's express 216 in terms of its prime factors:
\[
216 = 6^3,
\]
so we can rewrite \(216^x\) as
\[
216^x = (6^3)^x = 6^{3x}.
\]
Now, substituting this back into the equation gives us:
\[
\frac{1}{6^{(x+1)}} = 6^{3x}.
\]
Next, we can rewrite \(\frac{1}{6^{(x+1)}}\) as \(6^{-(x+1)}\), leading to:
\[
6^{-(x+1)} = 6^{3x}.
\]
Since the bases are the same, we can set the exponents equal to each other:
\[
-(x+1) = 3x.
\]
Now, we can solve for \(x\):
\[
-x - 1 = 3x.
\]
Adding \(x\) to both sides gives:
\[
-1 = 4x.
\]
Dividing both sides by 4 results in:
\[
x = -\frac{1}{4}.
\]
Thus, the solution to the equation \(\frac{1}{6^{(x+1)}} = 216^{(x)}\) is
\[
\boxed{-\frac{1}{4}}.
\]
-
0,5
-
1,25
-
5
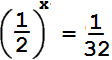
-
Давайте решим уравнение:
\[
\frac{1}{2^{(x)}} = \frac{1}{32}.
\]
Для начала, заметим, что \(32\) можно выразить через степень \(2\):
\[
32 = 2^5.
\]
Таким образом, мы можем переписать правую часть уравнения:
\[
\frac{1}{32} = \frac{1}{2^5}.
\]
Теперь уравнение выглядит так:
\[
\frac{1}{2^x} = \frac{1}{2^5}.
\]
Поскольку обе части имеют одну и ту же основу, мы можем приравнять показатели:
\[
-x = -5.
\]
Умножив обе стороны на \(-1\), получаем:
\[
x = 5.
\]
Таким образом, решение уравнения:
\[
\boxed{5}.
\]
18.
Найдите корень уравнения:
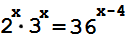
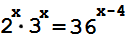
-
Для решения уравнения
\[
2^{(x)} \cdot 3^{(x)} = 36^{(x-4)},
\]
начнем с того, что \(36\) можно выразить через множители \(2\) и \(3\):
\[
36 = 6^2 = (2 \cdot 3)^2 = 2^2 \cdot 3^2.
\]
Таким образом, мы можем записать \(36^{(x-4)}\) как:
\[
36^{(x-4)} = (2^2 \cdot 3^2)^{(x-4)} = 2^{2(x-4)} \cdot 3^{2(x-4)} = 2^{(2x-8)} \cdot 3^{(2x-8)}.
\]
Теперь подставим это в исходное уравнение:
\[
2^{(x)} \cdot 3^{(x)} = 2^{(2x-8)} \cdot 3^{(2x-8)}.
\]
Теперь, так как основание одинаковое, мы можем приравнять показатели:
1. Для оснований \(2\):
\[
x = 2x - 8.
\]
Решим это уравнение:
\[
x - 2x = -8 \implies -x = -8 \implies x = 8.
\]
2. Для оснований \(3\):
\[
x = 2x - 8.
\]
Аналогично, мы получаем:
\[
x - 2x = -8 \implies -x = -8 \implies x = 8.
\]
Таким образом, для обоих случаев мы получаем одно и то же значение для \(x\).
В итоге, решение уравнения:
\[
\boxed{8}.
\]
19.
Найдите корень уравнения:
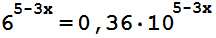
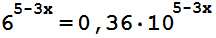
-
1
20.
Найдите корень уравнения:
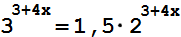
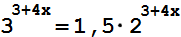
-
-0,5